|
|
|
The Fourier Transform converts information in the time domain into the frequency domain. It is an important analytical tool whenever it is necessary to determine the frequency components of a given time series waveform. The thumbnail theory is that any periodic waveform may be represented by a series of sine wave functions at different amplitudes, frequencies, and phase shifts which when summed together for each time series increment will reproduce the original waveform. Given an appropriate multi-term sine function (Fourier expansion) for a time series waveform, the magnitude of each term of the expansion may be plotted versus its frequency to yield a power spectrum that is representative of the frequency makeup of the time series waveform. The WinDaq Waveform Browser contains three types of Fourier transforms; the fast Fourier transform (FFT), the discrete Fourier transform (DFT), and the inverse Fourier transform (IFT).
The FFT is the most computationally efficient transform of the three but also the least versatile. The FFT function automatically places some restrictions on the time series to be evaluated. It requires that the range or length of waveform to be evaluated contains a total number of data points precisely equal to a power of 2 (e.g., 256, 512, 1024, etc.). Therefore, with an FFT you can only evaluate a fixed length waveform containing 512 points, or 1024 points, or 2048 points, etc. For example, if your time series contains 1096 data points, you would only be able to evaluate 1024 of them at a time using an FFT since 1024 is the highest 2n that is less than 1096. Additionally, the FFT also requires that the time series to be evaluated is a commensurate periodic function, or in other words, the time series must contain a whole number of periods within the FFT bounds. Obviously, the chances of a section of waveform containing a number of data points equal to a 2n number and having the last point match the first in magnitude and slope are slim at best. Significant distortion in the resulting power spectrum can result if care is not taken to ensure that end-points match as demonstrated by the following illustration:
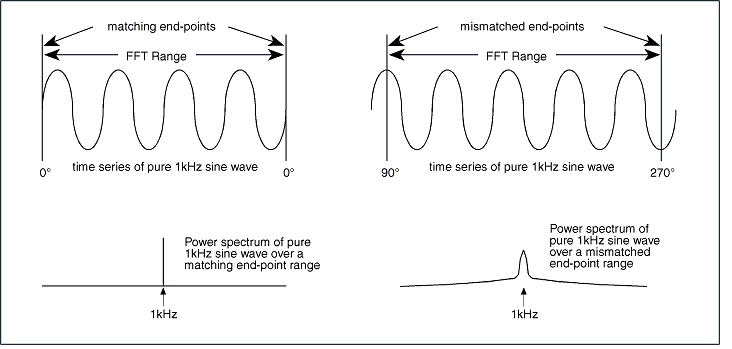
End-point mismatches over the FFT range can result in significant power spectrum distortion.
Fortunately a number of solutions exist to minimize the effects of end-point mismatches. One solution is to window the time series waveform so that the distortion is greatly attenuated or reduced to zero depending upon the window type. This approach multiplies the time series waveform by a function resembling a bell-shaped curve before applying the FFT. FFT Generation describes how windows may be applied to correct the power spectrum of time series waveforms generated over a number of points equal to a power of 2.
Another solution abandons windowing in favor of allowing the user to precisely define the range over which the transform is calculated. This approach nullifies the 2n limitation and is known as the DFT. Refer to Discrete Fourier Transform (DFT) for further information on Fourier transform generation over variable, user-defined ranges.
The IFT allows you to reconstruct the original signal (as a function of time) from the power spectrum (as a function of frequency). This capability makes power spectrum filtering possible. The IFT also comes in handy when determining what a certain power spectrum represents. Suppose you open a file that was saved and exited from the split screen Fourier transform utility. The screen will display the typical split screen Fourier transform mode with a power spectrum that you know very little about at first glance. The quickest way to find out what that power spectrum represents is to do an IFT and compare this result (displayed in window 2 of the Y-T area) with the original waveform in window 1 of the Y-T area. The IFT will show you the portion of the original waveform that was used to generate the power spectrum. Refer to Inverse Fourier Transformation (IFT) for further information on editing in the frequency domain.
Discrete Fourier Transform (DFT)
Inverse Fourier Transformation (IFT)
Exiting Fourier Transform Mode
Transform Calculation Time Considerations